Связь между максимизацией прибыли...

Связи между максимизацией прибыли, с одной стороны, и максимизацией рентабельности оборота, рентабельности издержек и экономичности, с другой стороны (первый случай: заданы предполагаемая функция цена - сбыт и линейная функция издержек; второй случай: заданы условия атомистической конкуренции и дегрессивно-прогрессивная функция издержек)

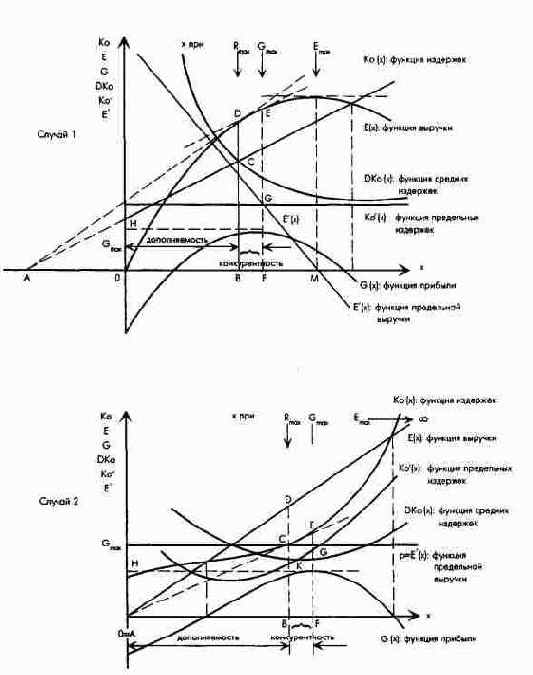
Для определения объема производства, максимизирующего рентабельность оборота, действует условие: